在十六世纪的欧洲,随着数学的繁荣,一元三次方程的求解方法也逐渐确立这一重要成就被赋予了一个名字“卡尔丹诺公式”,以纪念意大利数学先驱卡尔丹诺,他是世界上首位发表这一求根公式的人然而,卡尔丹诺并非一元三次方程通式解的首倡者事实上,早在中国的南宋时期,数学家秦九韶在1247年的。
经过多年的探索和研究,冯塔纳利用十分巧妙的方法,找到了一元三次方程一般形式的求根方法这个成就,使他在几次公开的数学较量中大获全胜,从此名扬欧洲但是冯塔纳不愿意将他的这个重要发现公之于世当时的另一位意大利数学家兼医生卡尔达诺卡尔丹诺,对冯塔纳的发现非常感兴趣他几次诚恳地登。
该公式在十六世纪由意大利数学家罗杰·卡尔丹提出,用于解析一元三次方程的根通过应用卡尔丹公式,可以找到方程的解,尽管这些解可能包括复数这一过程涉及复杂的代数操作,包括立方根的提取,是数学中一个引人入胜的领域在解决一元三次方程的过程中,首先需要对方程进行适当转换,以简化计算过程例如。
但是,很多数学史的书上只说阿里·花拉子模是世界上最先求得二次方程一般解的人,原因是丢番都当时认为只有根式下的数是一个完全平方时,方程才能算有解,并且丢番都只承认正根到了16世纪,意大利数学家卡尔丹和他的学生费尔拉利,相继发表了用根式求解三次方程与四次方程的方法卡尔丹在发表三次。
科学革命文艺复兴时期,科学领域发生了许多重大变革,艺术家创建的透视法对数学和几何学产生了深远影响三次方程解法16世纪的意大利,数学家们开始探索三次方程的解法1545年,意大利学者卡尔丹发表了三次方程的求根公式,这是数学史上的一大突破虚数与复数的理论发展卡尔丹的贡献卡尔丹不仅是第一。
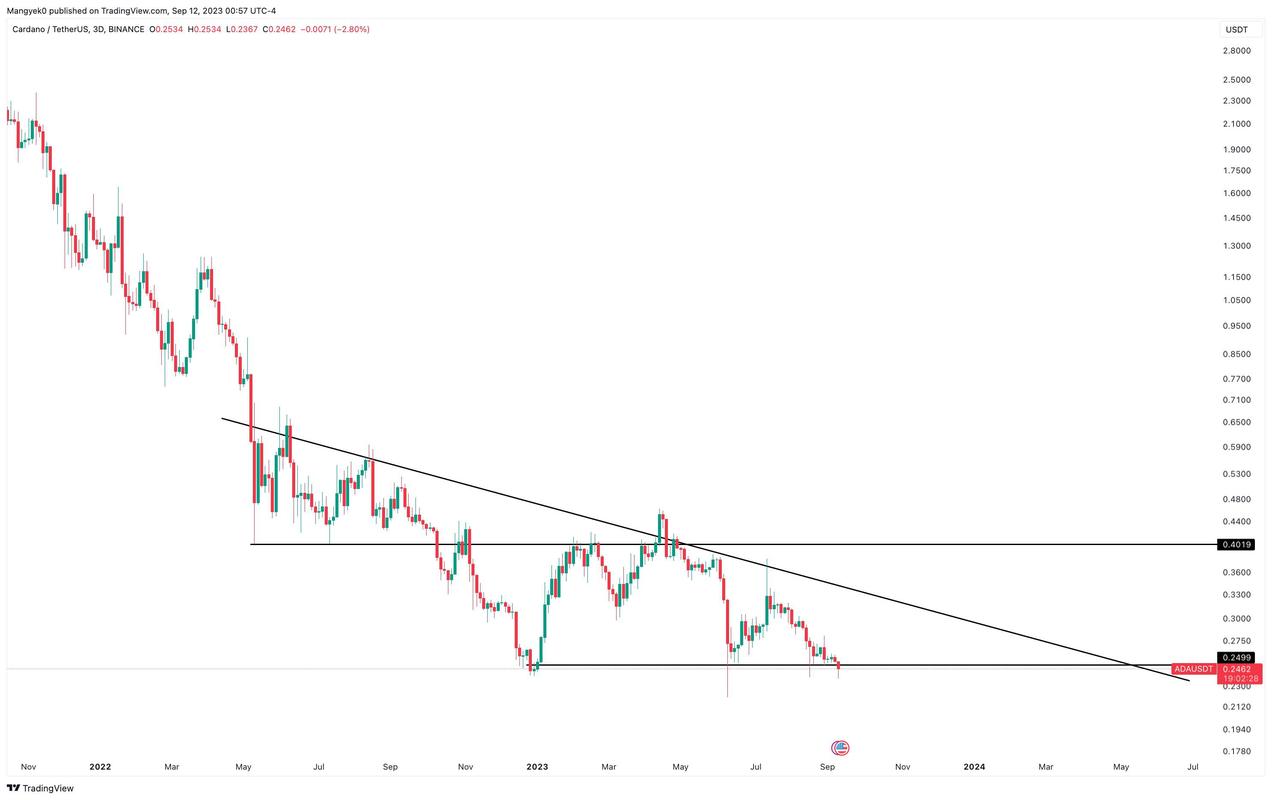
历史上,人类对于一元二次方程的求解技术早已熟知,但一元三次方程的研究却经历了较长的摸索期在古代,各个文明中心如中国希腊和印度,数学家们纷纷投身于这个难题的探索他们尝试发明各种解法,然而这些方法大多局限于特定类型的三次方程,对于一般的三次方程形式,却显得力不从心,无法给出通用的解。
随着数学的发展,数学家发现一些三次方程的实数根还非得用负数的平方根表示不可而且,如果承认了负数的平方根,那么代数方程的有无根问题就可以得到解决,并且会得出n次方程有n个根这样一个令人满意的结果此外,对负数的平方根按数的运算法则进行运算,结果也是正确的意大利数学家卡尔丹作出一个折中。